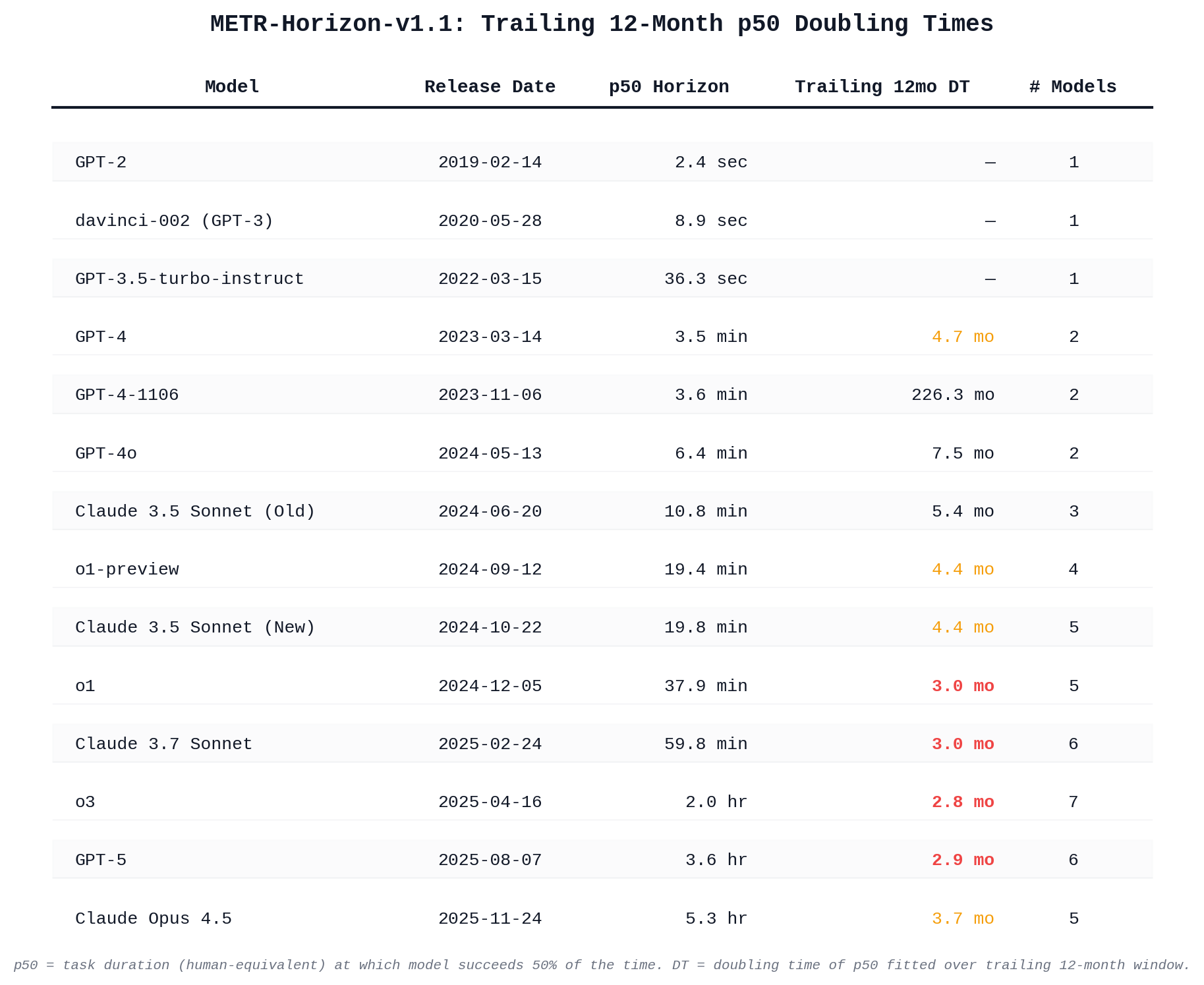
This market matches Software Engineering: METR Time Horizon Doubling Time from the AI 2026 Forecasting Survey by AI Digest.
See other manifold questions here

Resolution criteria
Resolves to the best-fit doubling time for METR-HRS frontier models as of December 31, 2026, computed using the methodology described in the More Info section of the survey (see here).
If METR releases an updated METR-HRS suite that is a clear successor with comparable difficulty for questions at the same horizon length, this question will be resolved based on the updated task suite.
Which AI systems count?
Any AI system counts if it operates within realistic deployment constraints and doesn't have unfair advantages over human baseliners.
Tool assistance, scaffolding, and any other inference-time elicitation techniques are permitted as long as:
No unfair and systematic advantage. There is no systematic unfair advantage over the humans described in the Human Performance section (e.g. AI systems are allowed to have multiple outputs autograded while humans aren't, or AI systems have access to the internet when humans don't).
Human cost parity. Having the AI system complete the task does not use more compute than could be purchased with the wages needed to pay a human to complete the same task to the same level. Any additional costs incurred by the AIs or humans (such as GPU rental costs) are included in the parity estimation.
The PASS@k elicitation technique (which automatically grades and chooses the best out of k outputs from a model) is a common example that we do not accept on this benchmark because human software engineers do not have access to automatic grading of their solutions, so PASS@k would constitute an unfair advantage.
If there is evidence of training contamination leading to substantially increased performance, scores will be accordingly adjusted or disqualified.
If a model is released in 2026 but evaluated after year-end, the resolver may include it at their discretion (if they think that there was not an unfair advantage from being evaluated later, for example the scaffolding used should have been available within 2026).
Eli Lifland is responsible for final judgment on resolution decisions.
Human cost estimation process:
Rank questions by human cost. For each question, estimate how much it would cost for humans to solve it. If humans fail on a question, factor in the additional cost required for them to succeed.
Match the AI's accuracy to a human cost total. If the AI system solves N% of questions, identify the cheapest N% of questions (by human cost) and sum those costs to determine the baseline human total.
Account for unsolved questions. For each question the AI does not solve, add the maximum cost from that bottom N%. This ensures both humans and AI systems are compared under a fixed per-problem budget, without relying on humans to dynamically adjust their approach based on difficulty.
Buckets are left-inclusive: e.g., 4-4.5 months includes 4.0 but not 4.5.
People are also trading
@bh wow jimreality is arriving sooner than some expected
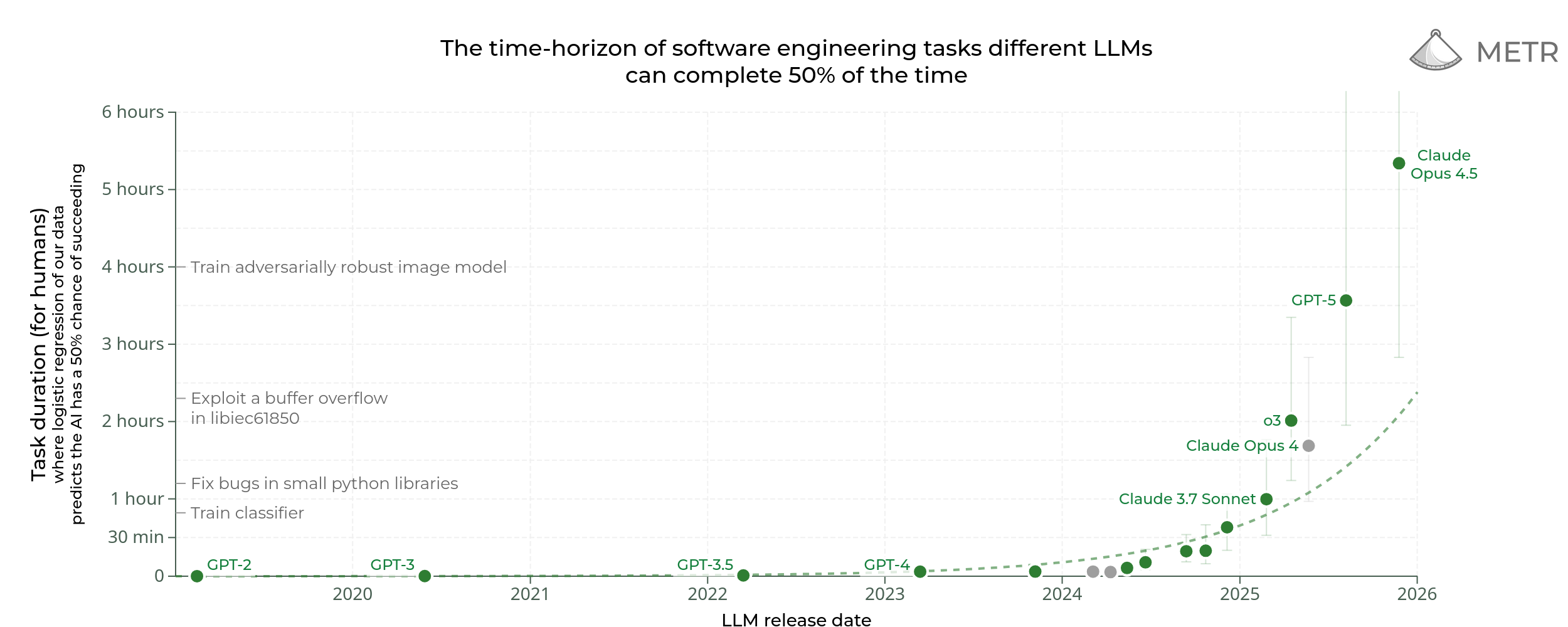
doubling time since 2024 is under three months (88.6 days)
@jim i asked claude code to make it using the data from METR’s website. it’s possible there are mistakes.
@bh The new graph has made think that by the end of the year we will see a SOTA model that has a time horizon length of somewhere between 24 to 30 hours.
@Bayesian my best guess for current doubling-times is 2.86 months, so this market should hopefully resolve in my favour. The measurement itself of model horizons this long is the main thing I'd be worried about (and I haven't read into exactly how the answer to this question will be determined yet) but what I've heard from METR about improving their task set is mostly reassuring.
@Bayesian true anyway I covered the 2.86 months thing on the bsky CoT. Read it, you'll laughing a lot
@Bayesian I am confused by how doubling time are determined. How would I determine the METR doubling time for 2026 if I think that the METR time horizon at the end of the year is going to be somewhere between 19 to 24 hours?
@MaxLennartson it isn't a function of only the time at the end of the year, it's the line of best fit across all the frontier datapoints across the entire year. so if it's 5 hours til september and then 20 hours in december that's very different from if it's 5 hours then 9 hours then 12 hours then 15 then 20, or something. but suppose it was the latter thing, it would be roughly 20/5 = 4x in a year, or ~6months of doubling time
@Bayesian So even if I think that by the end of year the highest time horizon will be somewhere between 19-24 hours. Does that mean the doubling time for the entire year could be any one of the answers up above?
@jim honestly I think pretty reasonable. I think it really depends how METR is operationalizing the tasks >>24 hours
@MaxLennartson yeah pretty much, though some of them much less likely than others. a reason to do this is that the metr time horizon measurements are pretty noisy so taking a line of best fit reduces that noise compared to taking the last point of 2026 and basing the prediction on that. eg if the highest time horizon is 22 hours, maybe that was a fluke, maybe it was measurement bias, etc.
@Bayesian Do you have any recommendations for how to go about deciding doubling time is the best fit?
@Bayesian Assuming 19-24 hours by end of the year. It seems unlikely that the doubling time would be less than three months but it could be 4.5, 5 or even 6 months. Does it come down to guessing or is there a strategy to choosing the doubling time?
@MaxLennartson the quickest estimate is to do 19-24hours divided by the current best score of 4h49min, that's your multiple per year, and then finding the doubling time from that, with some log2 math
@Bayesian ya but what if, like, the last 2026 measurement is 2150 hours because ClaudeCode Opus 5 just saturates the benchmark by autonomously making a SimCity game or something, idk
I swear people just look at what doubling times have been recently and say to themselves, "Yeah, they'll probably stay around that". Are people not aware that doubling times are obviously, predictably, and observably decreasing? If your forecast is "I think doubling times will stay roughly the same" then IMO you haven't succeeded in thinking well about the problem.
I would not be even slightly surprised to see unbounded time-horizons by EOY.
@Bayesian I am still a bit confused. Maybe I am doing my math wrong. I did 19 hours divided by 4 hours 49 minutes. I got 3.94463668 (3 hours 56 minutes 41 seconds). 3.94463668 log2 came out to 1.979892427. Does this number mean 1 months of doubling time in other words less than 3 months?
@MaxLennartson dividing hours by hours gets you a dimensionless quantity which represents the number of times bigger that later time horizon is than the earlier one. So time horizon increased 3.94463668 times in a year. Then the log math is that log2(3.94463668) = 1.97989 repredents the number of doublings in a year, so the inverse is the number of years in a doubling, so 1/1.97989 ~= 0.5, is the doubling time in years. Converting to months it is nearly 6 months of doubling time.